library(StanHeaders)
library(ggplot2)
library(rstan)
rstan_options(auto_write = TRUE)
# 如果CPU和内存足够,设置成与马尔科夫链一样多
options(mc.cores = max(c(floor(parallel::detectCores() / 2), 1L)))
custom_colors <- c(
"#4285f4", # GoogleBlue
"#34A853", # GoogleGreen
"#FBBC05", # GoogleYellow
"#EA4335" # GoogleRed
)
rstan_ggtheme_options(
panel.background = element_rect(fill = "white"),
legend.position = "top"
)
rstan_gg_options(
fill = "#4285f4", color = "white",
pt_color = "#EA4335", chain_colors = custom_colors
)34 分层正态模型
介绍分层正态模型的定义、结构、估计,分层正态模型与线性生长模型的关系,分层正态模型与潜变量模型的关系,分层正态模型与神经网络模型的关系,以 rstan 包和 nlme 包实现简单分层正态模型,说明 rstan 包的一些用法,比较贝叶斯参数估计和频率参数估计的结果,给出结果的解释。
34.1 8schools 数据
8schools 数据最早来自 Rubin (1981)
分层正态模型
\[ \begin{aligned} y_j &\sim \mathcal{N}(\theta_j,\sigma_j) \quad \theta_j = \mu + \tau * \eta_j \\ \theta_j &\sim \mathcal{N}(\mu, \tau) \quad \eta_j \sim \mathcal{N}(0,1) \end{aligned} \]
34.1.1 拟合模型
用 rstan 包来拟合模型
# 编译模型
eight_schools_fit <- stan(
model_name = "eight_schools",
# file = "code/8schools.stan",
model_code = "
// saved as 8schools.stan
data {
int<lower=0> J; // number of schools
real y[J]; // estimated treatment effects
real<lower=0> sigma[J]; // standard error of effect estimates
}
parameters {
real mu; // population treatment effect
real<lower=0> tau; // standard deviation in treatment effects
vector[J] eta; // unscaled deviation from mu by school
}
transformed parameters {
vector[J] theta = mu + tau * eta; // school treatment effects
}
model {
target += normal_lpdf(eta | 0, 1); // prior log-density
target += normal_lpdf(y | theta, sigma); // log-likelihood
}
",
data = list( # 观测数据
J = 8,
y = c(28, 8, -3, 7, -1, 1, 18, 12),
sigma = c(15, 10, 16, 11, 9, 11, 10, 18)
),
warmup = 1000, # 每条链预处理迭代次数
iter = 2000, # 每条链总迭代次数
chains = 2, # 马尔科夫链的数目
cores = 2, # 指定 CPU 核心数,可以给每条链分配一个
verbose = FALSE, # 不显示迭代的中间过程
refresh = 0, # 不显示采样的进度
seed = 20190425 # 设置随机数种子,不要使用 set.seed() 函数
)#> Warning: There were 1 divergent transitions after warmup. See
#> https://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
#> to find out why this is a problem and how to eliminate them.#> Warning: Examine the pairs() plot to diagnose sampling problems34.1.2 模型输出
#> Inference for Stan model: eight_schools.
#> 2 chains, each with iter=2000; warmup=1000; thin=1;
#> post-warmup draws per chain=1000, total post-warmup draws=2000.
#>
#> mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
#> mu 8.2 0.2 5.1 -1.2 4.8 8.0 11.3 19.1 975 1
#> tau 6.6 0.2 5.8 0.3 2.5 5.3 9.2 20.7 784 1
#> eta[1] 0.4 0.0 0.9 -1.5 -0.2 0.4 1.0 2.2 1696 1
#> eta[2] -0.1 0.0 0.8 -1.7 -0.6 0.0 0.5 1.7 1748 1
#> eta[3] -0.2 0.0 0.9 -2.0 -0.8 -0.2 0.3 1.7 1921 1
#> eta[4] 0.0 0.0 0.9 -1.7 -0.7 -0.1 0.6 1.7 2035 1
#> eta[5] -0.4 0.0 0.9 -2.0 -1.0 -0.4 0.2 1.4 1859 1
#> eta[6] -0.2 0.0 0.9 -1.9 -0.8 -0.3 0.4 1.6 1885 1
#> eta[7] 0.3 0.0 0.8 -1.4 -0.2 0.3 0.9 2.0 1743 1
#> eta[8] 0.0 0.0 0.9 -1.7 -0.6 0.0 0.6 1.9 2118 1
#> theta[1] 11.4 0.2 8.2 -2.0 6.1 10.3 15.3 31.1 1194 1
#> theta[2] 7.8 0.1 6.2 -4.3 4.1 7.7 11.4 20.3 2314 1
#> theta[3] 6.0 0.2 7.5 -10.6 2.0 6.5 10.7 19.7 1698 1
#> theta[4] 7.7 0.1 6.6 -6.2 3.8 7.7 11.6 21.4 2052 1
#> theta[5] 5.2 0.1 6.4 -9.3 1.3 5.8 9.4 16.2 2025 1
#> theta[6] 6.2 0.1 6.6 -8.0 2.6 6.6 10.5 18.9 2106 1
#> theta[7] 10.5 0.2 6.5 -1.3 6.3 10.0 14.2 25.0 1566 1
#> theta[8] 8.2 0.2 7.7 -8.0 3.9 8.1 12.5 24.2 1764 1
#> lp__ -39.4 0.1 2.6 -44.8 -41.0 -39.2 -37.6 -34.8 752 1
#>
#> Samples were drawn using NUTS(diag_e) at Mon Oct 16 10:50:27 2023.
#> For each parameter, n_eff is a crude measure of effective sample size,
#> and Rhat is the potential scale reduction factor on split chains (at
#> convergence, Rhat=1).提取任意一个参数的结果,如查看参数 \(\tau\) 的 95% 置信区间。
#> Inference for Stan model: eight_schools.
#> 2 chains, each with iter=2000; warmup=1000; thin=1;
#> post-warmup draws per chain=1000, total post-warmup draws=2000.
#>
#> mean se_mean sd 2.5% 97.5% n_eff Rhat
#> tau 6.65 0.21 5.76 0.27 20.73 784 1
#>
#> Samples were drawn using NUTS(diag_e) at Mon Oct 16 10:50:27 2023.
#> For each parameter, n_eff is a crude measure of effective sample size,
#> and Rhat is the potential scale reduction factor on split chains (at
#> convergence, Rhat=1).从迭代抽样数据获得与 print(fit) 一样的结果。以便后续对原始采样数据做任意的进一步分析。rstan 包扩展泛型函数 summary() 以支持对 stanfit 数据对象汇总,输出各个参数分链条和合并链条的后验分布结果。
34.1.3 操作数据
合并四条马氏链的结果
返回的结果是一个列表
#> List of 5
#> $ mu : num [1:2000(1d)] -0.349 13.214 4.653 8.459 4.314 ...
#> ..- attr(*, "dimnames")=List of 1
#> .. ..$ iterations: NULL
#> $ tau : num [1:2000(1d)] 5.171 0.281 3.416 4.26 6.84 ...
#> ..- attr(*, "dimnames")=List of 1
#> .. ..$ iterations: NULL
#> $ eta : num [1:2000, 1:8] 0.8443 0.1824 -0.5421 0.3176 0.0592 ...
#> ..- attr(*, "dimnames")=List of 2
#> .. ..$ iterations: NULL
#> .. ..$ : NULL
#> $ theta: num [1:2000, 1:8] 4.02 13.27 2.8 9.81 4.72 ...
#> ..- attr(*, "dimnames")=List of 2
#> .. ..$ iterations: NULL
#> .. ..$ : NULL
#> $ lp__ : num [1:2000(1d)] -37.8 -42.5 -41.8 -36.5 -36 ...
#> ..- attr(*, "dimnames")=List of 1
#> .. ..$ iterations: NULL#> [1] "list"计算参数 \(\eta,\theta\) 的均值
#> [1] 0.37737234 -0.05115180 -0.22331030 -0.04388245 -0.35811384 -0.22323565
#> [7] 0.30601563 0.01891633#> [1] 11.436791 7.793837 6.010571 7.703675 5.161396 6.237395 10.528707
#> [8] 8.185503计算参数 \(\eta,\theta\) 的分位点
#>
#> 2.5% 25% 50% 75% 97.5%
#> [1,] -1.507198 -0.1968247 0.37869013 0.9789101 2.174623
#> [2,] -1.726116 -0.5851447 -0.04740783 0.4768830 1.660240
#> [3,] -1.994936 -0.8202685 -0.23339301 0.3494418 1.662723
#> [4,] -1.745175 -0.6545073 -0.05512642 0.5521324 1.741359
#> [5,] -2.004906 -0.9575384 -0.35962354 0.2032693 1.407583
#> [6,] -1.922606 -0.8169963 -0.25524392 0.3566269 1.574648
#> [7,] -1.368122 -0.2396888 0.31536228 0.8581667 1.970735
#> [8,] -1.736231 -0.5953672 -0.03530469 0.6294982 1.886066#>
#> 2.5% 25% 50% 75% 97.5%
#> [1,] -2.033648 6.100229 10.271452 15.343849 31.06742
#> [2,] -4.273520 4.050181 7.722681 11.445376 20.34221
#> [3,] -10.641025 1.990698 6.517992 10.713881 19.70925
#> [4,] -6.152792 3.824841 7.651704 11.638808 21.40971
#> [5,] -9.289988 1.294042 5.751342 9.403381 16.21893
#> [6,] -8.003669 2.607037 6.582900 10.452106 18.90089
#> [7,] -1.262546 6.306058 9.995780 14.187053 25.04851
#> [8,] -7.978283 3.895587 8.129171 12.493753 24.21741计算参数 \(\mu,\tau\) 的均值
#> $mu
#> [1] 8.180393#> $tau
#> [1] 6.647675#> $lp__
#> [1] -39.38927计算参数 \(\mu,\tau\) 的分位点
#> $mu
#> 2.5% 25% 50% 75% 97.5%
#> -1.218135 4.824075 7.972065 11.343782 19.089152#> $tau
#> 2.5% 25% 50% 75% 97.5%
#> 0.2686822 2.4555350 5.3460596 9.1916895 20.7314381#> $lp__
#> 2.5% 25% 50% 75% 97.5%
#> -44.77153 -41.00192 -39.23531 -37.59843 -34.8090734.1.4 采样诊断
获取马尔科夫链迭代点列数据
eight_schools_sim 是一个三维数组,1000(次迭代)* 2 (条链)* 19(个参数)。如果 permuted = TRUE 则会合并四条马氏链的迭代结果,变成一个列表。
#> [1] "array"#> num [1:1000, 1:2, 1:19] 14.07 13.02 9.03 8.03 6.85 ...
#> - attr(*, "dimnames")=List of 3
#> ..$ iterations: NULL
#> ..$ chains : chr [1:2] "chain:1" "chain:2"
#> ..$ parameters: chr [1:19] "mu" "tau" "eta[1]" "eta[2]" ...提取参数 \(\mu\) 的四条迭代点列
matplot(eight_schools_mu_sim,
xlab = "Iteration", ylab = expression(mu),
type = "l", lty = "solid", col = custom_colors
)
abline(h = apply(eight_schools_mu_sim, 2, mean), col = custom_colors)
legend("bottomleft",
legend = paste0("chain:", 1:2), box.col = "white", inset = 0.01,
lty = "solid", horiz = TRUE, col = custom_colors
)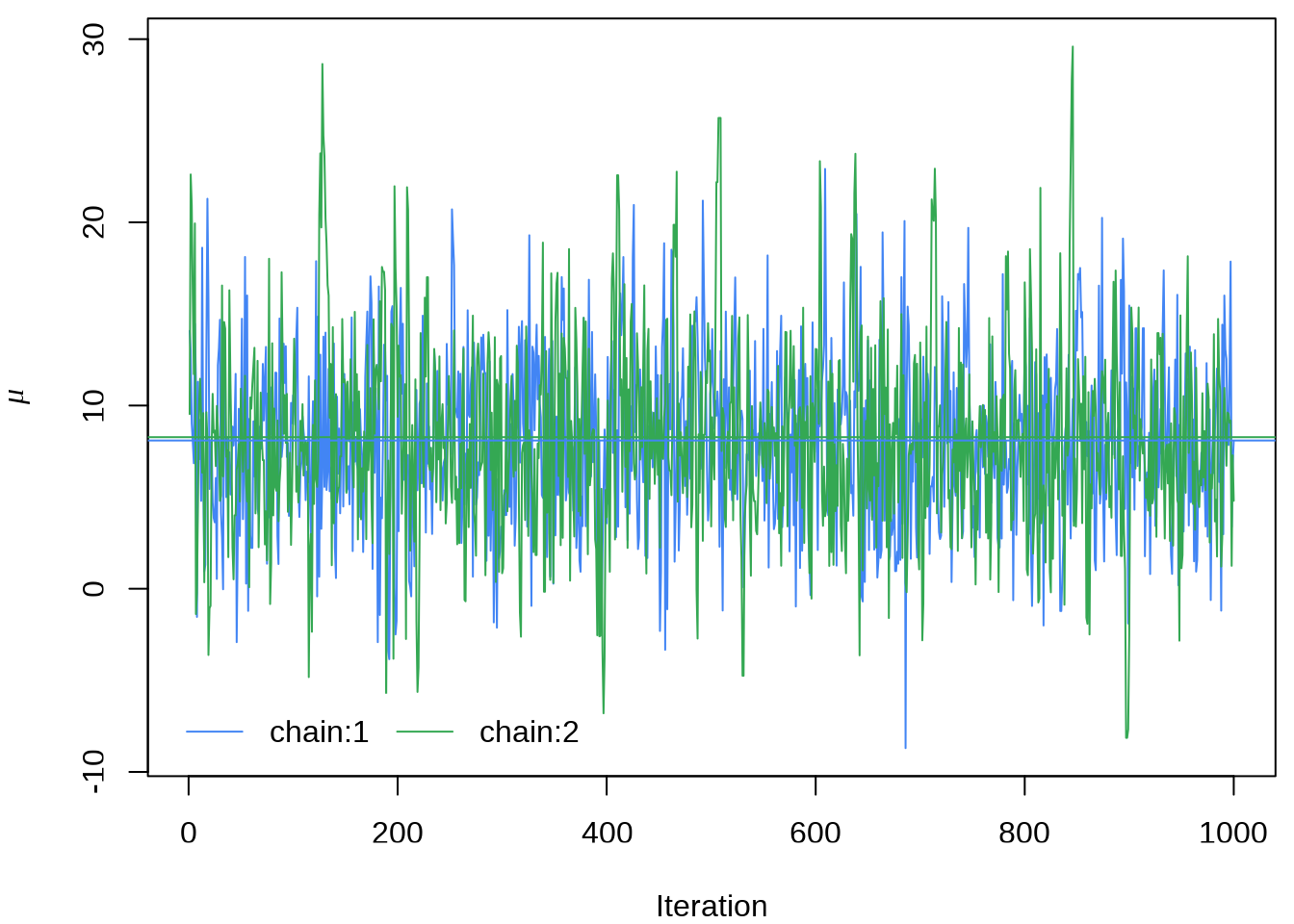
或者使用 rstan 提供的 traceplot 函数或者 stan_trace 函数,rstan 大量依赖 ggplot2 绘图,所以如果你熟悉 GGplot2 可以很方便地定制属于自己的风格,除了 rstan 提供的 rstan_ggtheme_options 和 rstan_gg_options 两个函数外,还可以使用 ggplot2 自带的大量配置选项和主题,如 theme_minimal 主题,因为 stan_trace等作图函数返回的是一个 ggplot 对象。
stan_trace(eight_schools_fit, pars = "mu") +
theme_minimal() +
labs(x = "Iteration", y = expression(mu))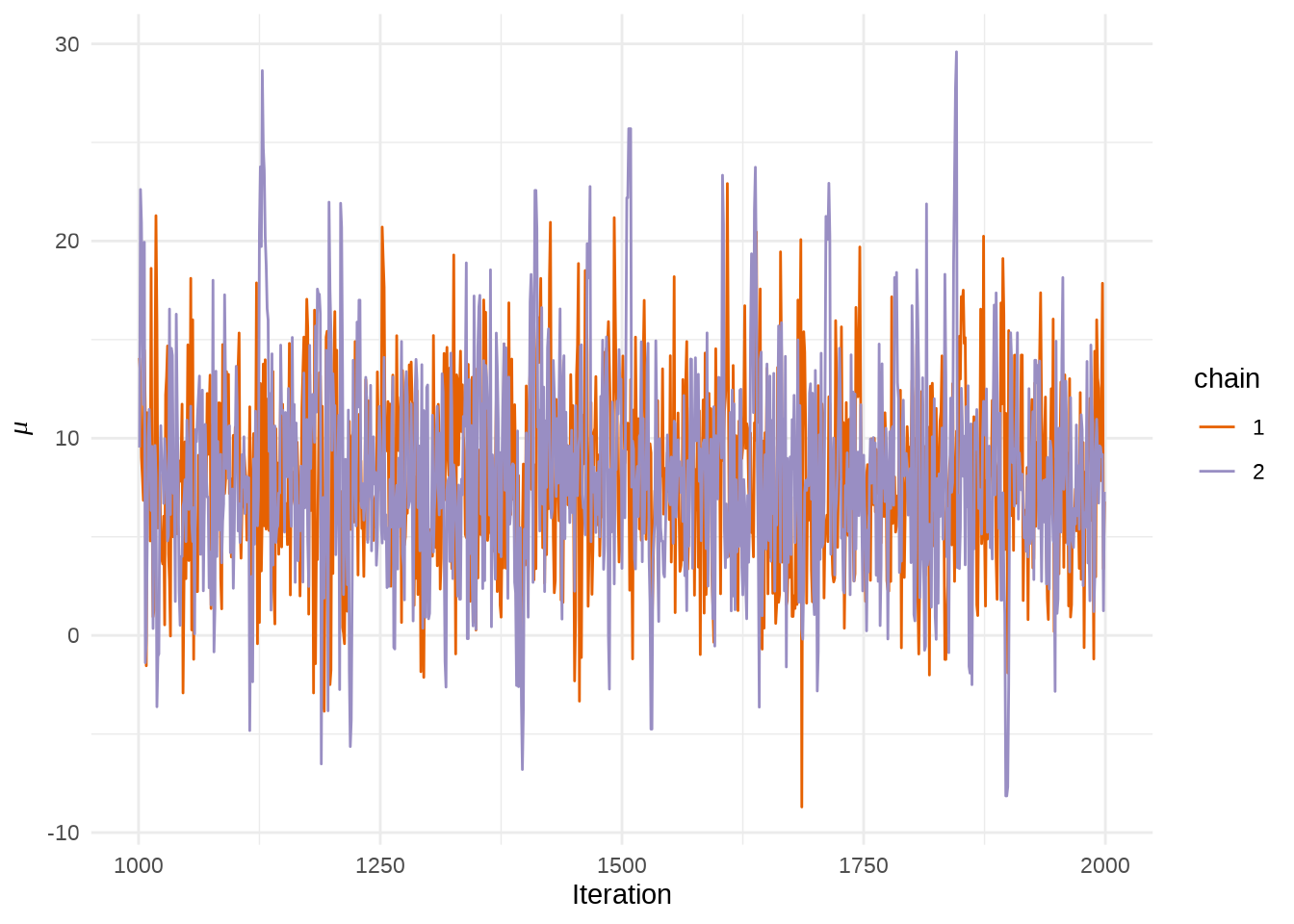
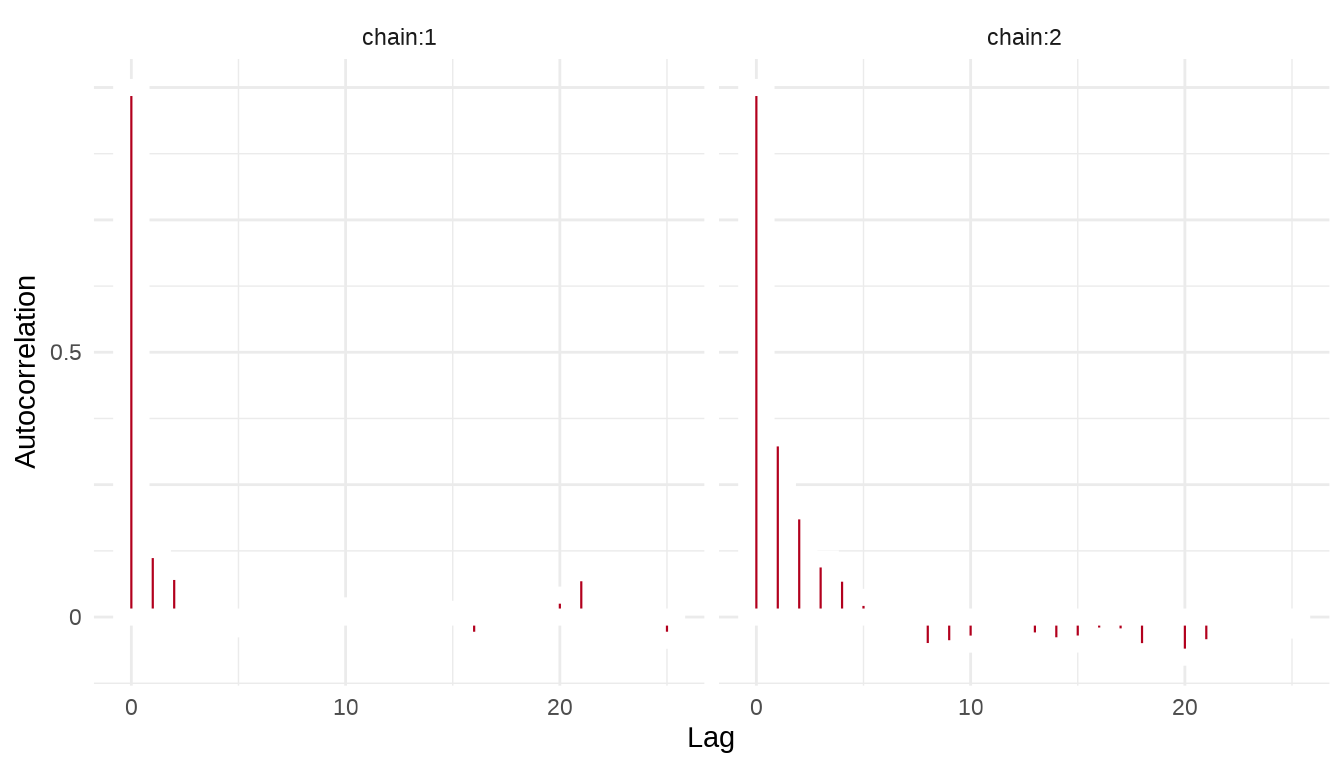
序列的自相关图,类似地,我们这里也使用 stan_ac 函数绘制自相关图
34.1.5 后验分布
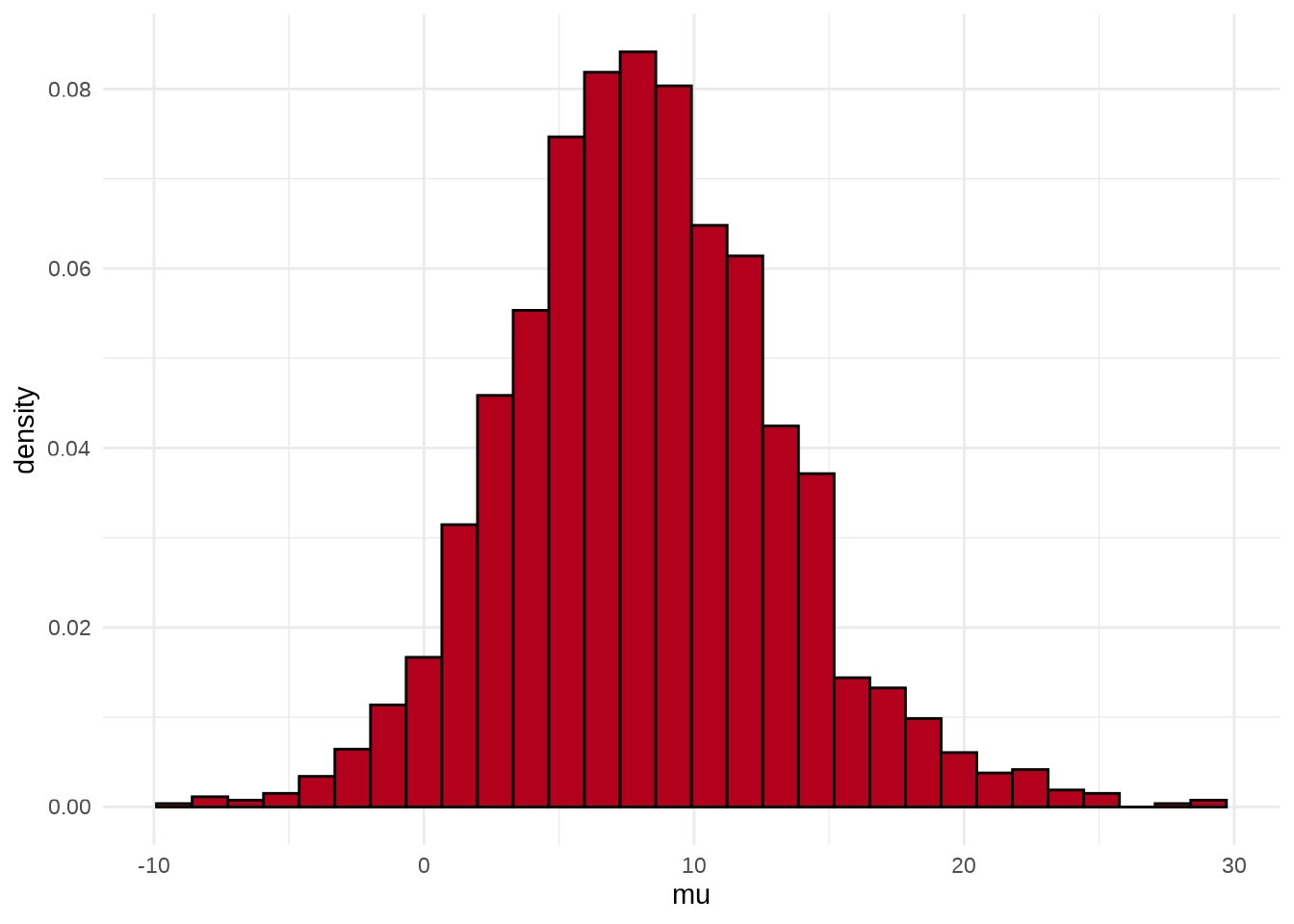
可以用 stan_hist 函数绘制参数 \(\mu\) 的后验分布图,它没有 separate_chains 参数,所以不能分链条绘制
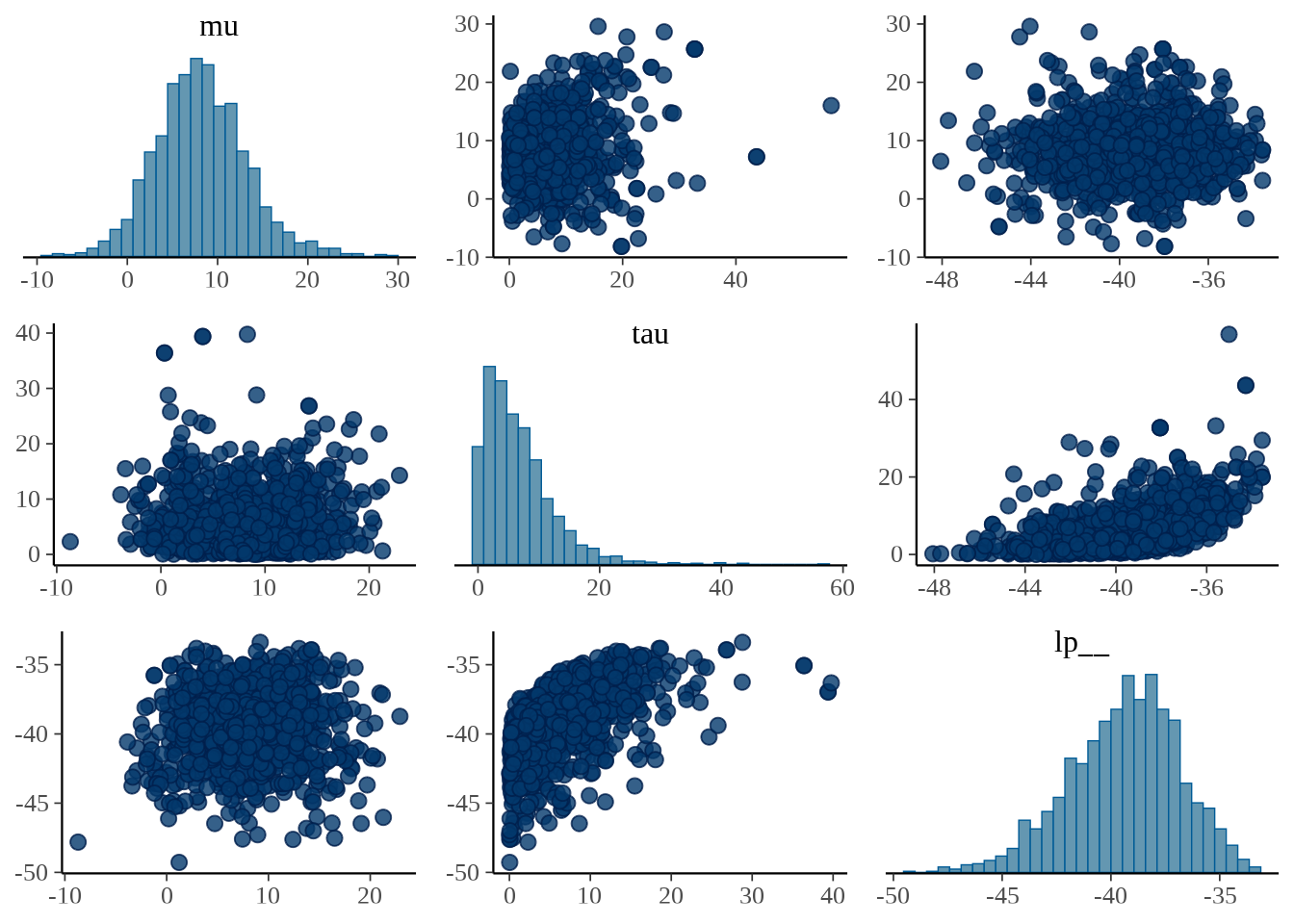
参数 \(\mu\) 和 \(\tau\) 的散点图
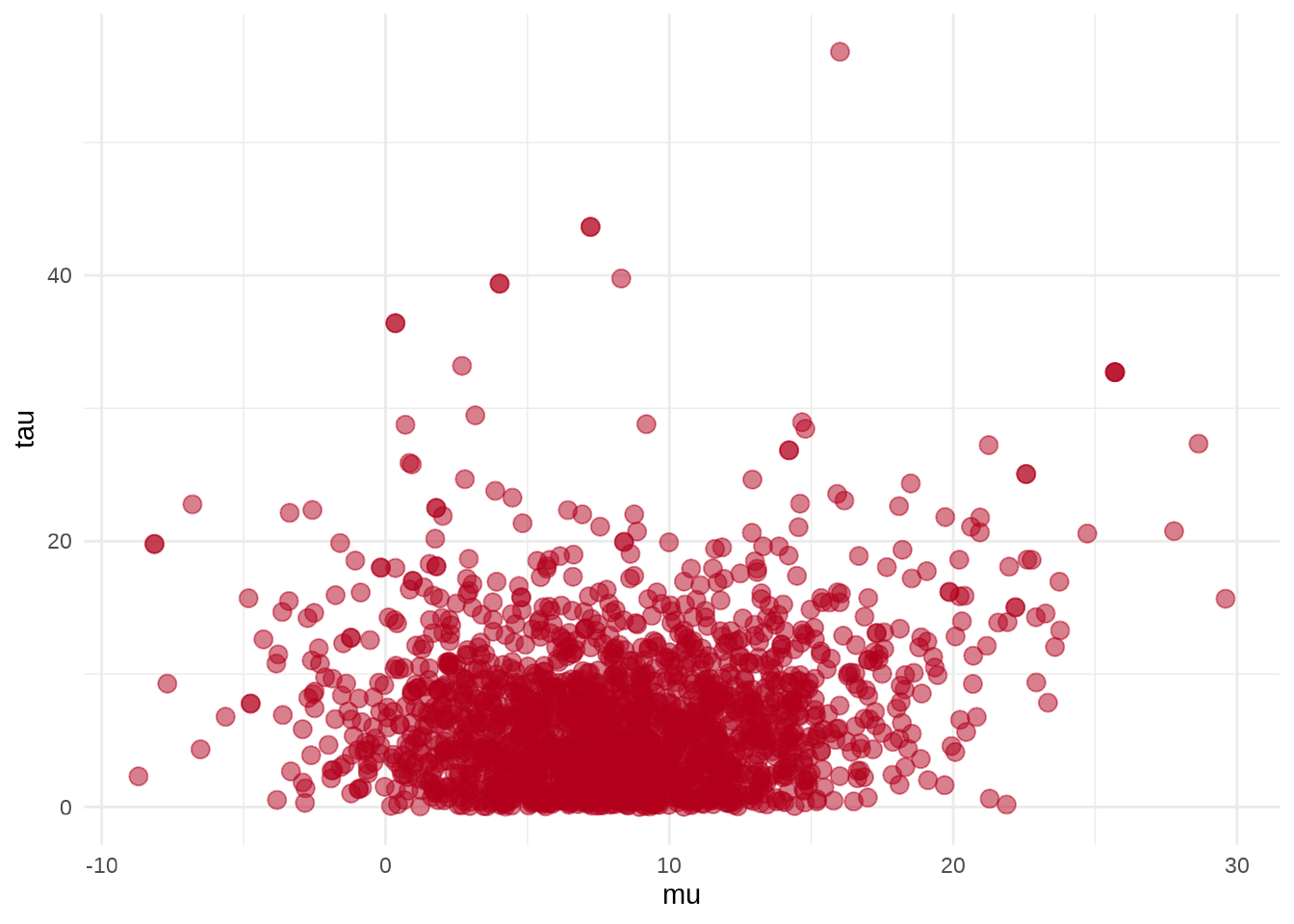
参数 \(\mu\) 的后验概率密度分布图
stan_dens(eight_schools_fit, pars = "mu", separate_chains = TRUE) +
theme_minimal() +
labs(x = expression(mu), y = "Density")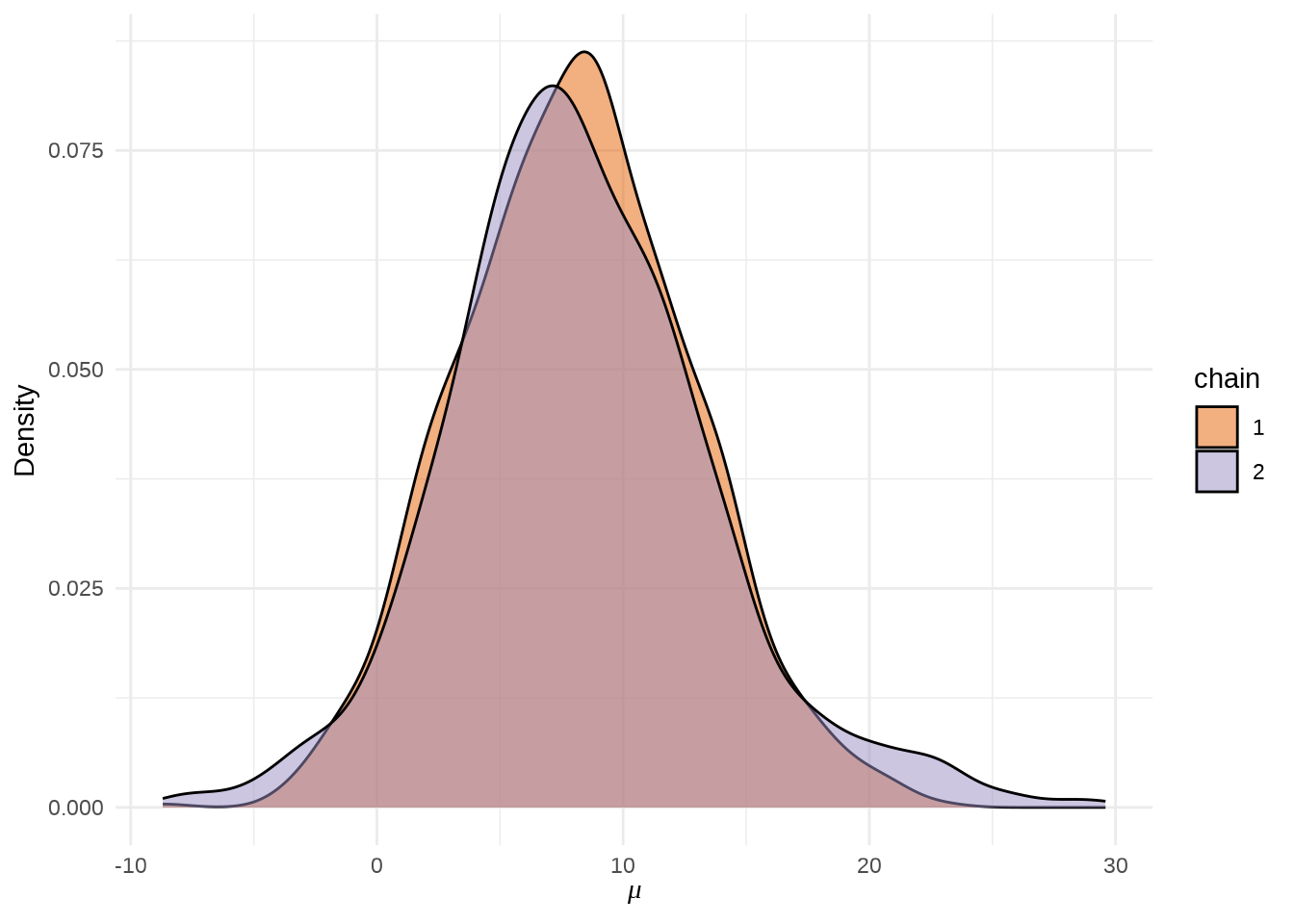
bayesplot 包的函数 mcmc_pairs() 以矩阵图展示多个参数的分布。
34.1.6 其它 R 包
接下来,分别用 nlme 和 lme4 包拟合模型。
首先,调用 nlme 包的函数 lme() 拟合模型。
library(nlme)
fit_lme <- lme(y ~ 1, random = ~ 1 | g, weights = varFixed(~ sigma^2), method = "REML")
summary(fit_lme)#> Linear mixed-effects model fit by REML
#> Data: NULL
#> AIC BIC logLik
#> 60.21091 60.04864 -27.10546
#>
#> Random effects:
#> Formula: ~1 | g
#> (Intercept) Residual
#> StdDev: 2.917988 0.780826
#>
#> Variance function:
#> Structure: fixed weights
#> Formula: ~sigma^2
#> Fixed effects: y ~ 1
#> Value Std.Error DF t-value p-value
#> (Intercept) 7.785729 3.368082 8 2.311621 0.0496
#>
#> Standardized Within-Group Residuals:
#> Min Q1 Med Q3 Max
#> -1.06635035 -0.73588511 -0.02896764 0.50254917 1.62502386
#>
#> Number of Observations: 8
#> Number of Groups: 8随机效应的标准差 2.917988 ,随机效应部分的估计
#> (Intercept)
#> 1 1.18135690
#> 2 0.02625714
#> 3 -0.55795544
#> 4 -0.08130333
#> 5 -1.29202241
#> 6 -0.70215328
#> 7 1.25167648
#> 8 0.17414393类比 Stan 输出结果中的 \(\theta\) 向量,每个学校的成绩估计
#> (Intercept)
#> 1 11.232914
#> 2 7.862347
#> 3 6.157622
#> 4 7.548487
#> 5 4.015623
#> 6 5.736854
#> 7 11.438106
#> 8 8.293879接着,采用 lme4 包拟合模型,发现 lme4 包获得与 nlme 包一样的结果。
control <- lme4::lmerControl(
check.conv.singular = "ignore",
check.nobs.vs.nRE = "ignore",
check.nobs.vs.nlev = "ignore"
)
fit_lme4 <- lme4::lmer(y ~ 1 + (1 | g), weights = 1 / sigma^2, control = control, REML = TRUE)
summary(fit_lme4)#> Linear mixed model fit by REML ['lmerMod']
#> Formula: y ~ 1 + (1 | g)
#> Weights: 1/sigma^2
#> Control: control
#>
#> REML criterion at convergence: 54.2
#>
#> Scaled residuals:
#> Min 1Q Median 3Q Max
#> -1.06635 -0.73589 -0.02897 0.50255 1.62502
#>
#> Random effects:
#> Groups Name Variance Std.Dev.
#> g (Intercept) 8.5145 2.9180
#> Residual 0.6097 0.7808
#> Number of obs: 8, groups: g, 8
#>
#> Fixed effects:
#> Estimate Std. Error t value
#> (Intercept) 7.786 3.368 2.312最后,使用 blme 包 (Chung 等 2013) ,blme 包基于 lme4 包,截距项结果比较一致,随机效应(组间方差)和残差项(组内方差)完全不同。
### Example using a residual variance prior ###
# This is the "eight schools" data set;
# the mode should be at the boundary of the space.
fit_blme <- blme::blmer(
y ~ 1 + (1 | g),
control = control, REML = TRUE,
resid.prior = point, cov.prior = NULL,
weights = 1 / sigma^2
)
summary(fit_blme)#> Resid prior: point(value = 1)
#> Prior dev : 0
#>
#> Linear mixed model fit by REML ['blmerMod']
#> Formula: y ~ 1 + (1 | g)
#> Weights: 1/sigma^2
#> Control: control
#>
#> REML criterion at convergence: 54.7
#>
#> Scaled residuals:
#> Min 1Q Median 3Q Max
#> -0.96507 -0.62280 -0.01545 0.43763 1.35429
#>
#> Random effects:
#> Groups Name Variance Std.Dev.
#> g (Intercept) 8.583e-19 9.264e-10
#> Residual 1.000e+00 1.000e+00
#> Number of obs: 8, groups: g, 8
#>
#> Fixed effects:
#> Estimate Std. Error t value
#> (Intercept) 7.686 4.072 1.88734.2 rats 数据
rats 数据最早来自 Gelfand 等 (1990) ,记录 30 只小鼠每隔一周的重量,一共进行了 5 周。第一次记录是小鼠第 8 天的时候,第二次测量记录是第 15 天的时候,一直持续到第 36 天。下面在 R 环境中准备数据。
# 总共 30 只老鼠
N <- 30
# 总共进行 5 周
T <- 5
# 小鼠重量
y <- structure(c(
151, 145, 147, 155, 135, 159, 141, 159, 177, 134,
160, 143, 154, 171, 163, 160, 142, 156, 157, 152, 154, 139, 146,
157, 132, 160, 169, 157, 137, 153, 199, 199, 214, 200, 188, 210,
189, 201, 236, 182, 208, 188, 200, 221, 216, 207, 187, 203, 212,
203, 205, 190, 191, 211, 185, 207, 216, 205, 180, 200, 246, 249,
263, 237, 230, 252, 231, 248, 285, 220, 261, 220, 244, 270, 242,
248, 234, 243, 259, 246, 253, 225, 229, 250, 237, 257, 261, 248,
219, 244, 283, 293, 312, 272, 280, 298, 275, 297, 350, 260, 313,
273, 289, 326, 281, 288, 280, 283, 307, 286, 298, 267, 272, 285,
286, 303, 295, 289, 258, 286, 320, 354, 328, 297, 323, 331, 305,
338, 376, 296, 352, 314, 325, 358, 312, 324, 316, 317, 336, 321,
334, 302, 302, 323, 331, 345, 333, 316, 291, 324
), .Dim = c(30, 5))
# 第几天
x <- c(8.0, 15.0, 22.0, 29.0, 36.0)
xbar <- 22.0重复测量的小鼠重量数据 rats 如下 表格 34.1 所示。
| 第 8 天 | 第 15 天 | 第 22 天 | 第 29 天 | 第 36 天 | |
|---|---|---|---|---|---|
| 1 | 151 | 199 | 246 | 283 | 320 |
| 2 | 145 | 199 | 249 | 293 | 354 |
| 3 | 147 | 214 | 263 | 312 | 328 |
| 4 | 155 | 200 | 237 | 272 | 297 |
| 5 | 135 | 188 | 230 | 280 | 323 |
| 6 | 159 | 210 | 252 | 298 | 331 |
小鼠重量数据的分布情况见下 图 34.8 ,由图可以假定 30 只小鼠的重量服从正态分布。
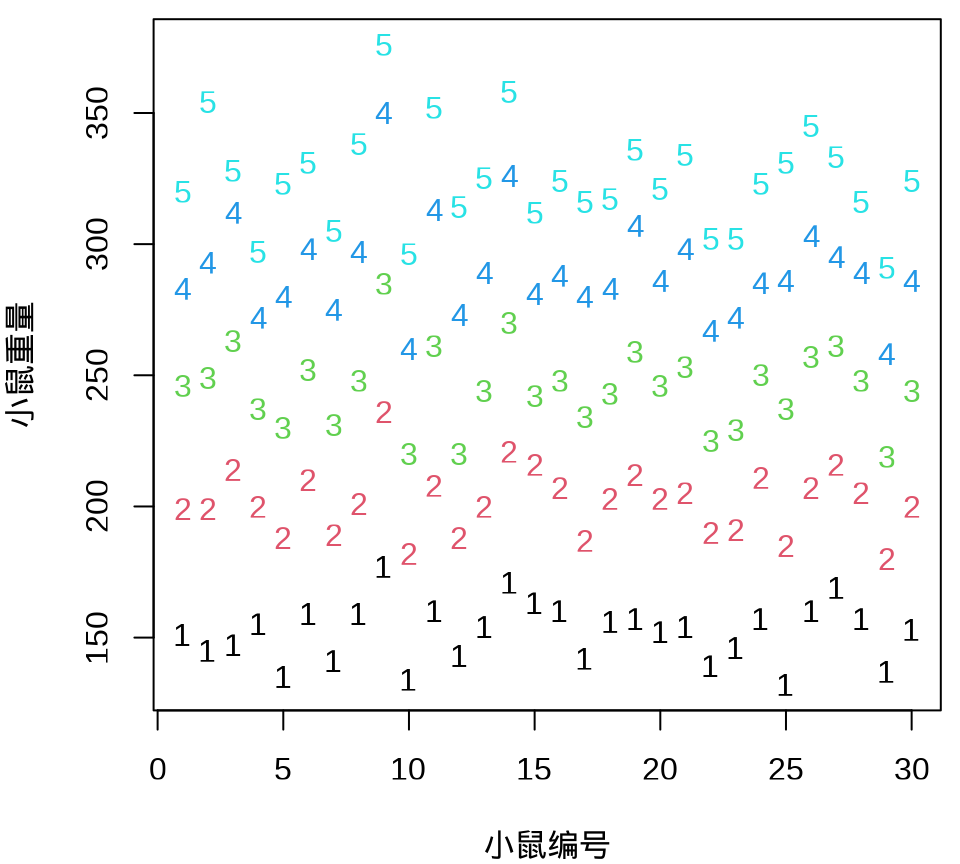
由 图 34.9 可见, 30 只小鼠的重量增长趋势呈现一种线性趋势。
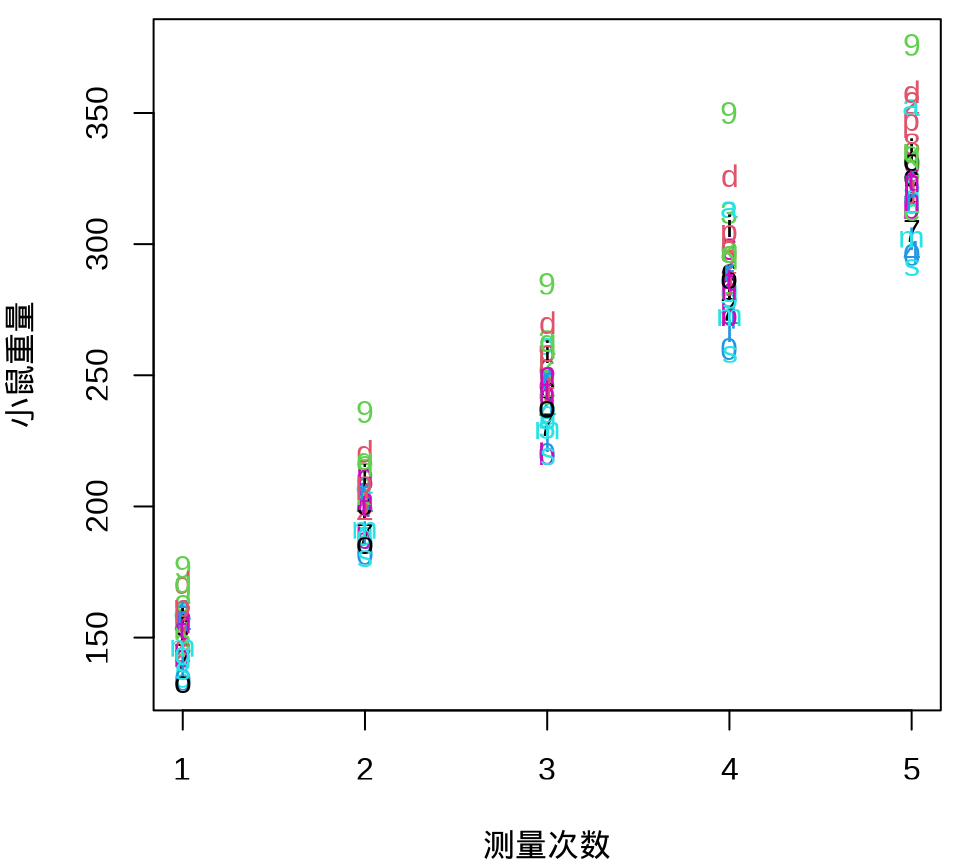
34.2.1 rstan
初始化模型参数,设置采样算法的参数。
接下来,基于重复测量数据,建立线性生长曲线模型:
\[ \begin{aligned} \alpha_c &\sim \mathcal{N}(0,100) \quad \beta_c \sim \mathcal{N}(0,100) \\ \tau^2_{\alpha} &\sim \mathrm{inv\_gamma}(0.001, 0.001) \\ \tau^2_{\beta} &\sim \mathrm{inv\_gamma}(0.001, 0.001) \\ \tau^2_c &\sim \mathrm{inv\_gamma}(0.001, 0.001) \\ \alpha_n &\sim \mathcal{N}(\alpha_c, \tau_{\alpha}) \quad \beta_n \sim \mathcal{N}(\beta_c, \tau_{\beta}) \\ y_{nt} &\sim \mathcal{N}(\alpha_n + \beta_n * (x_t - \bar{x}), \tau_c) \\ & n = 1,2,\ldots,N \quad t = 1,2,\ldots,T \end{aligned} \]
其中, \(\alpha_c,\beta_c,\tau_c,\tau_{\alpha},\tau_{\beta}\) 为无信息先验,\(\bar{x} = 22\) 表示第 22 天,\(N = 30\) 和 \(T = 5\) 分别表示实验中的小鼠数量和测量次数,下面采用 Stan 编码、编译、采样和拟合模型。
rats_fit <- stan(
model_name = "rats",
model_code = "
data {
int<lower=0> N;
int<lower=0> T;
vector[T] x;
matrix[N,T] y;
real xbar;
}
parameters {
vector[N] alpha;
vector[N] beta;
real alpha_c;
real beta_c; // beta.c in original bugs model
real<lower=0> tausq_c;
real<lower=0> tausq_alpha;
real<lower=0> tausq_beta;
}
transformed parameters {
real<lower=0> tau_c; // sigma in original bugs model
real<lower=0> tau_alpha;
real<lower=0> tau_beta;
tau_c = sqrt(tausq_c);
tau_alpha = sqrt(tausq_alpha);
tau_beta = sqrt(tausq_beta);
}
model {
alpha_c ~ normal(0, 100);
beta_c ~ normal(0, 100);
tausq_c ~ inv_gamma(0.001, 0.001);
tausq_alpha ~ inv_gamma(0.001, 0.001);
tausq_beta ~ inv_gamma(0.001, 0.001);
alpha ~ normal(alpha_c, tau_alpha); // vectorized
beta ~ normal(beta_c, tau_beta); // vectorized
for (n in 1:N)
for (t in 1:T)
y[n,t] ~ normal(alpha[n] + beta[n] * (x[t] - xbar), tau_c);
}
generated quantities {
real alpha0;
alpha0 = alpha_c - xbar * beta_c;
}
",
data = list(N = N, T = T, y = y, x = x, xbar = xbar),
chains = chains, init = init, iter = iter,
verbose = FALSE, refresh = 0, seed = 20190425
)模型输出结果如下:
#> Inference for Stan model: rats.
#> 4 chains, each with iter=1000; warmup=500; thin=1;
#> post-warmup draws per chain=500, total post-warmup draws=2000.
#>
#> mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
#> alpha_c 242.5 0.1 2.6 237.3 240.8 242.5 244.2 247.6 2200 1
#> beta_c 6.2 0.0 0.1 6.0 6.1 6.2 6.3 6.4 2134 1
#> tausq_c 37.3 0.2 5.4 28.3 33.4 36.8 40.5 49.0 1090 1
#> tausq_alpha 218.5 1.5 62.1 127.3 174.5 207.2 252.1 369.2 1787 1
#> tausq_beta 0.3 0.0 0.1 0.1 0.2 0.3 0.3 0.5 1340 1
#> tau_c 6.1 0.0 0.4 5.3 5.8 6.1 6.4 7.0 1096 1
#> tau_alpha 14.6 0.0 2.0 11.3 13.2 14.4 15.9 19.2 1871 1
#> tau_beta 0.5 0.0 0.1 0.4 0.5 0.5 0.6 0.7 1304 1
#> alpha0 106.4 0.1 3.5 99.4 104.0 106.4 108.7 113.4 2300 1
#> lp__ -438.6 0.3 6.6 -452.7 -442.9 -438.1 -434.1 -426.3 703 1
#>
#> Samples were drawn using NUTS(diag_e) at Mon Oct 16 10:51:58 2023.
#> For each parameter, n_eff is a crude measure of effective sample size,
#> and Rhat is the potential scale reduction factor on split chains (at
#> convergence, Rhat=1).alpha_c 表示小鼠 5 次测量的平均重量,beta_c 表示小鼠体重的增长率,\(\alpha_i,\beta_i\) 分别表示第 \(i\) 只小鼠在第 22 天(第 3 次测量或 \(x_t = \bar{x}\) )的重量和增长率(每日增加的重量)。
对于分量众多的参数向量,比较适合用岭线图展示后验分布,下面调用 bayesplot 包绘制参数向量 \(\boldsymbol{\alpha},\boldsymbol{\beta}\) 的后验分布。
# plot(rats_fit, pars = "alpha", show_density = TRUE, ci_level = 0.8, outer_level = 0.95)
bayesplot::mcmc_areas_ridges(rats_fit, pars = paste0("alpha", "[", 1:30, "]")) +
scale_y_discrete(labels = scales::parse_format()) 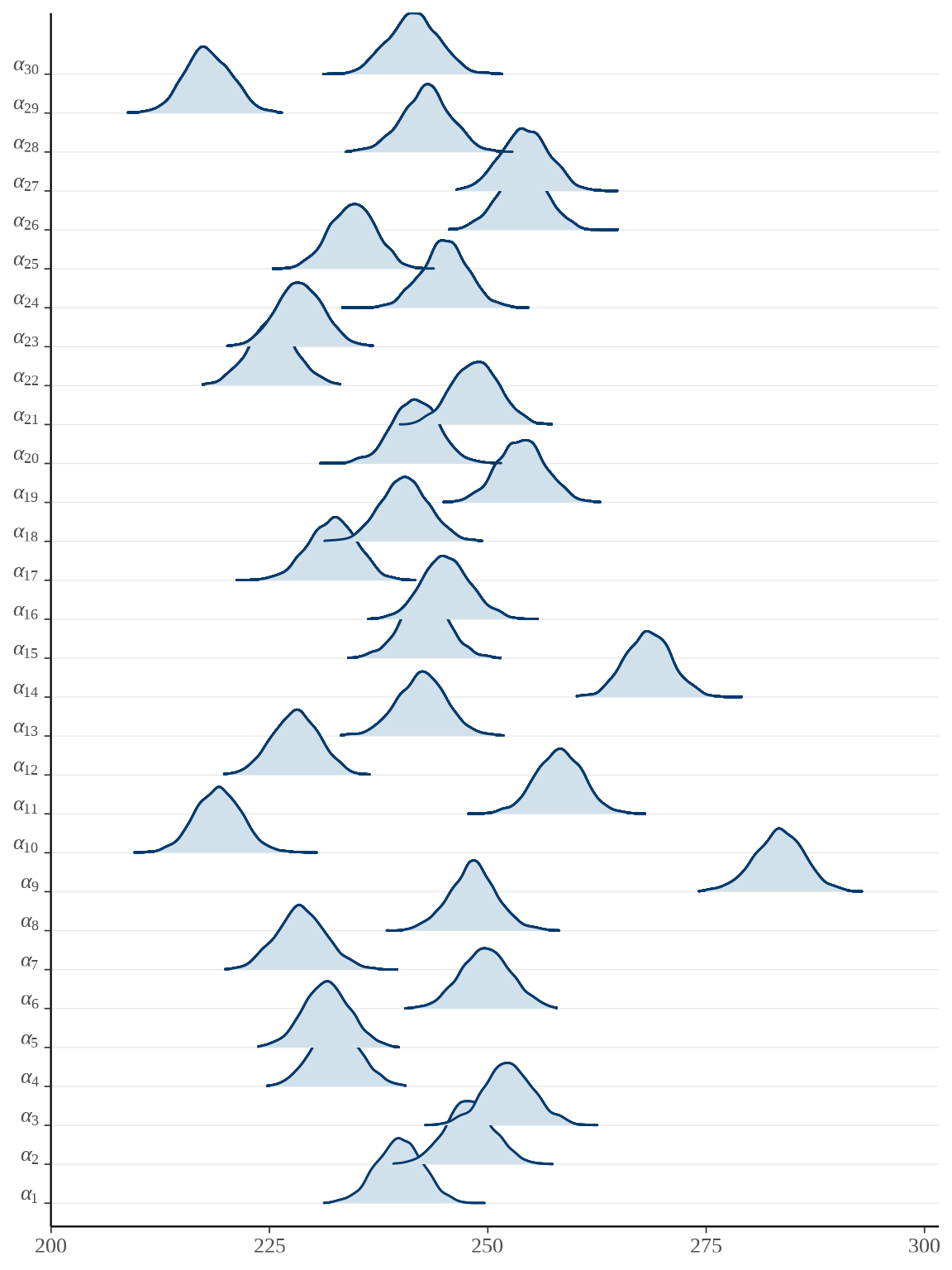
参数向量 \(\boldsymbol{\alpha}\) 的后验估计可以看作 \(x_t = \bar{x}\) 时小鼠的重量,上图即为各个小鼠重量的后验分布。
# plot(rats_fit, pars = "beta", ci_level = 0.8, outer_level = 0.95)
bayesplot::mcmc_areas_ridges(rats_fit, pars = paste0("beta", "[", 1:30, "]")) +
scale_y_discrete(labels = scales::parse_format()) 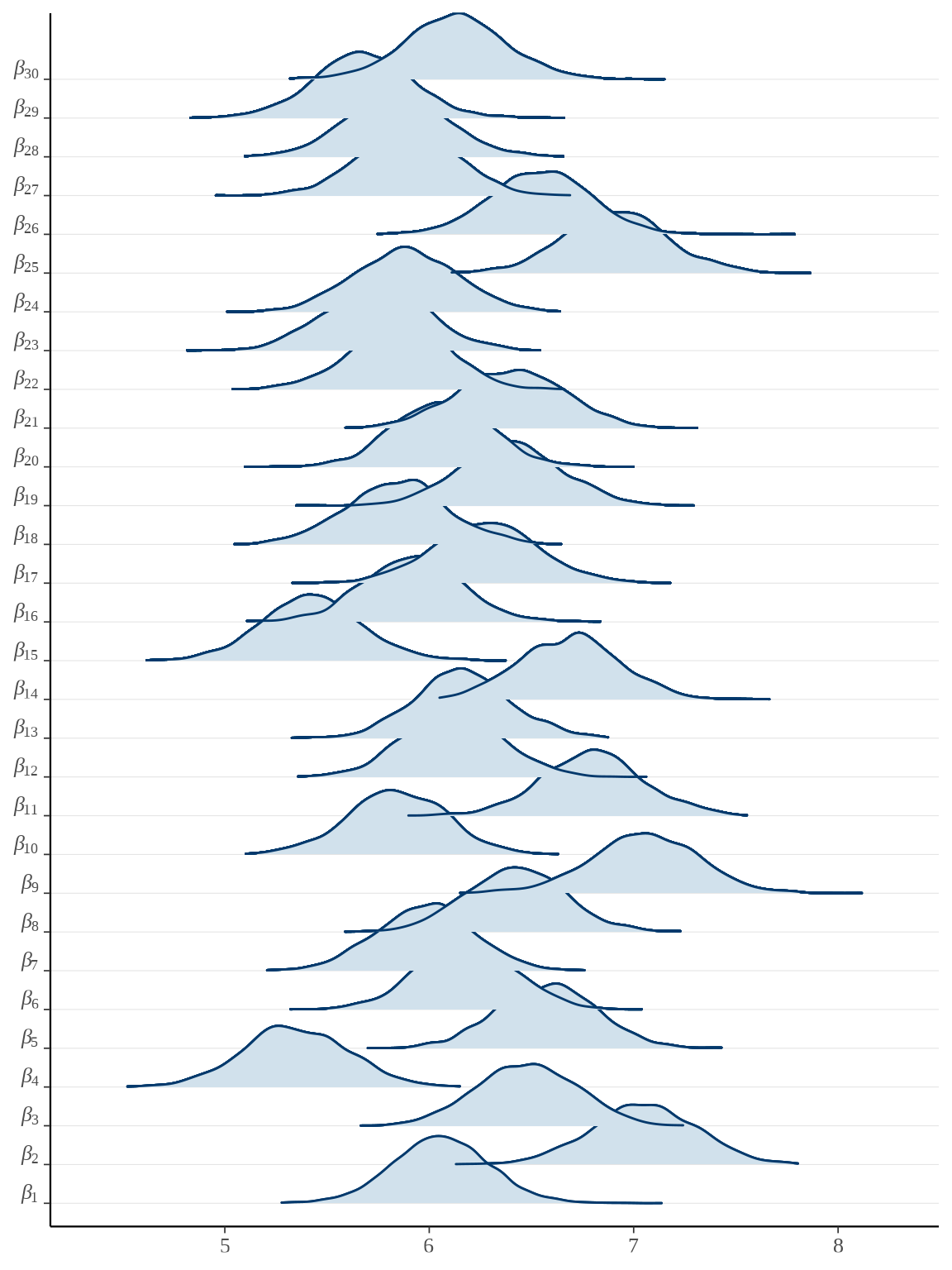
参数向量 \(\boldsymbol{\beta}\) 的后验估计可以看作是小鼠的重量的增长率,上图即为各个小鼠重量的增长率的后验分布。
34.2.2 lavaan
lavaan 包 (Rosseel 2012) 的函数 growth() 可以直接拟合曲线生长模型
其中,i 表示截距, s 表示斜率。下面拟合模型
模型输出
#> lavaan 0.6.16 ended normally after 173 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 10
#>
#> Number of observations 30
#>
#> Model Test User Model:
#>
#> Test statistic 68.986
#> Degrees of freedom 10
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> i =~
#> t1 1.000
#> t2 1.000
#> t3 1.000
#> t4 1.000
#> t5 1.000
#> s =~
#> t1 0.000
#> t2 1.000
#> t3 2.000
#> t4 3.000
#> t5 4.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> i ~~
#> s 10.625 9.304 1.142 0.253
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .t1 0.000
#> .t2 0.000
#> .t3 0.000
#> .t4 0.000
#> .t5 0.000
#> i 155.759 2.065 75.437 0.000
#> s 44.525 0.808 55.080 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .t1 32.762 12.914 2.537 0.011
#> .t2 13.005 5.219 2.492 0.013
#> .t3 5.181 3.498 1.481 0.139
#> .t4 17.105 8.426 2.030 0.042
#> .t5 157.548 45.272 3.480 0.001
#> i 112.957 33.179 3.404 0.001
#> s 15.909 5.124 3.105 0.00234.2.3 nlme
nlme 包适合长格式的数据,因此,先将小鼠数据整理成长格式。
weight <- c(
151, 145, 147, 155, 135, 159, 141, 159, 177, 134,
160, 143, 154, 171, 163, 160, 142, 156, 157, 152, 154, 139, 146,
157, 132, 160, 169, 157, 137, 153, 199, 199, 214, 200, 188, 210,
189, 201, 236, 182, 208, 188, 200, 221, 216, 207, 187, 203, 212,
203, 205, 190, 191, 211, 185, 207, 216, 205, 180, 200, 246, 249,
263, 237, 230, 252, 231, 248, 285, 220, 261, 220, 244, 270, 242,
248, 234, 243, 259, 246, 253, 225, 229, 250, 237, 257, 261, 248,
219, 244, 283, 293, 312, 272, 280, 298, 275, 297, 350, 260, 313,
273, 289, 326, 281, 288, 280, 283, 307, 286, 298, 267, 272, 285,
286, 303, 295, 289, 258, 286, 320, 354, 328, 297, 323, 331, 305,
338, 376, 296, 352, 314, 325, 358, 312, 324, 316, 317, 336, 321,
334, 302, 302, 323, 331, 345, 333, 316, 291, 324
)
rats <- rep(1:30, times = 5)
days <- rep(c(8, 15, 22, 29, 36), each = 30)
rats_data <- data.frame(weight = weight, rats = rats, days = days)将 30 只小鼠的重量变化及回归曲线画出来,发现各只小鼠的回归线的斜率几乎一样,截距略有不同。不同小鼠的出生重量是不同,前面 Stan 采用变截距变斜率的混合效应模型拟合数据。
ggplot(data = rats_data, aes(x = days, y = weight)) +
geom_point() +
geom_smooth(formula = "y ~ x", method = "lm", se = FALSE) +
theme_bw() +
facet_wrap(facets = ~rats, labeller = "label_both", ncol = 6) +
labs(x = "第几天", y = "重量")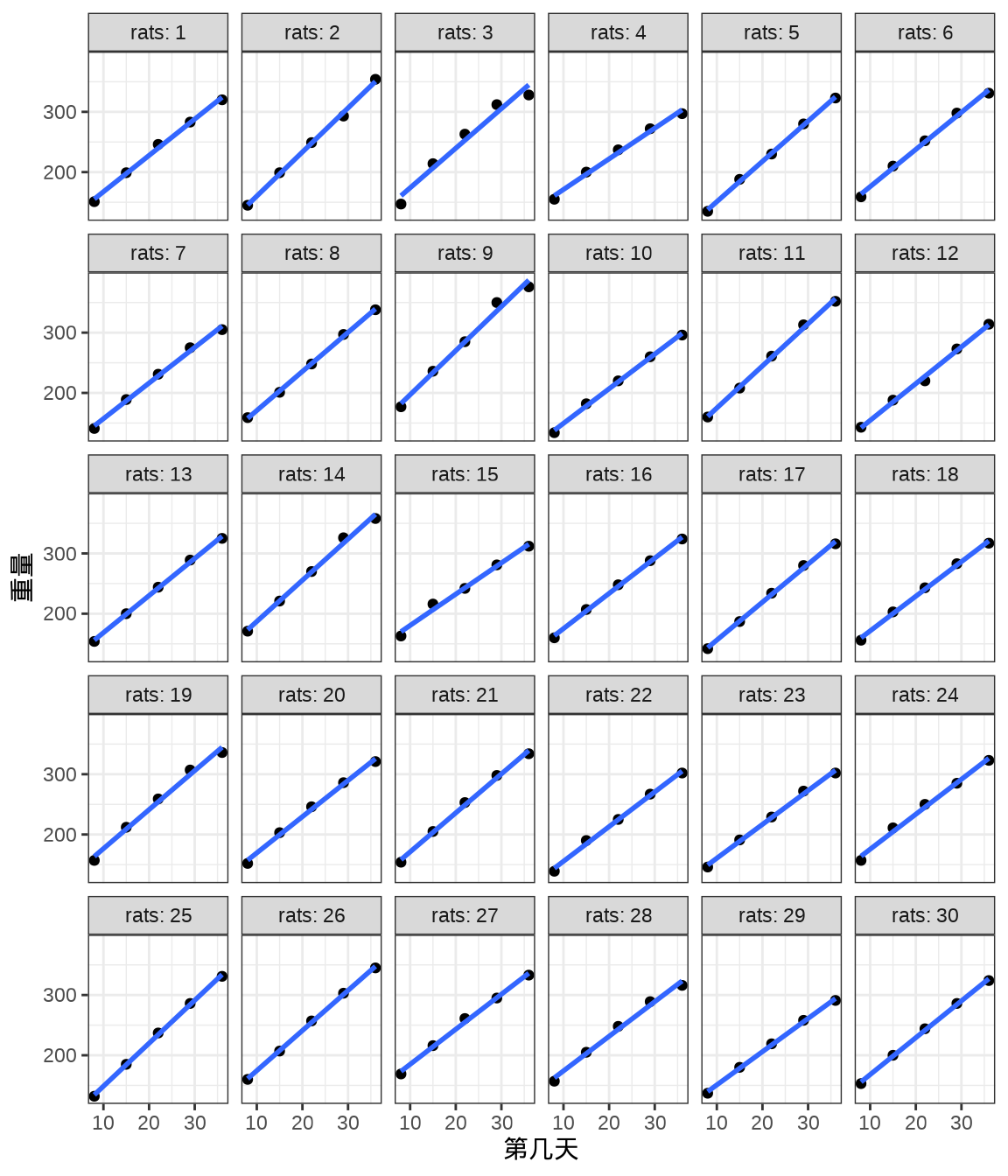
小鼠的重量随时间增长,不同小鼠的情况又会有所不同。可用随机效应模型表示生长曲线模型,下面加载 nlme 包调用函数 lme() 拟合该模型。
library(nlme)
rats_lme <- lme(data = rats_data, fixed = weight ~ days, random = ~ days | rats)
summary(rats_lme)#> Linear mixed-effects model fit by REML
#> Data: rats_data
#> AIC BIC logLik
#> 1107.373 1125.357 -547.6867
#>
#> Random effects:
#> Formula: ~days | rats
#> Structure: General positive-definite, Log-Cholesky parametrization
#> StdDev Corr
#> (Intercept) 10.7429538 (Intr)
#> days 0.5105284 -0.159
#> Residual 6.0146581
#>
#> Fixed effects: weight ~ days
#> Value Std.Error DF t-value p-value
#> (Intercept) 106.56762 2.2976758 119 46.38062 0
#> days 6.18571 0.1055885 119 58.58321 0
#> Correlation:
#> (Intr)
#> days -0.343
#>
#> Standardized Within-Group Residuals:
#> Min Q1 Med Q3 Max
#> -2.6370711 -0.5394662 0.1187649 0.4927166 2.6090856
#>
#> Number of Observations: 150
#> Number of Groups: 30模型输出结果中,固定效应中的截距项 (Intercept) 对应 106.56762,斜率 days 对应 6.18571。Stan 模型中截距参数 alpha0 的后验估计是 106.332,斜率参数 beta_c 的后验估计是 6.188。对比 Stan 和 nlme 包的拟合结果,可以发现贝叶斯和频率方法的结果是非常接近的。截距参数 alpha0 可以看作小鼠的初始(出生)重量,斜率参数 beta_c 可以看作小鼠的生长率 growth rate。
函数 lme() 的输出结果中,随机效应的随机截距标准差 10.7425835,对应 tau_alpha,表示每个小鼠的截距偏移量的波动。而随机斜率的标准差为 0.5105447,对应 tau_beta,相对随机截距标准差来说很小。残差标准差为 6.0146608,对应 tau_c,表示与小鼠无关的剩余量的波动,比如测量误差。总之,和 Stan 的结果有所不同,但相去不远。主要是前面的 Stan 模型没有考虑随机截距和随机斜率之间的相关性,这可以进一步调整 (Sorensen, Hohenstein, 和 Vasishth 2016) 。
Stan 输出中,截距项 alpha、斜率项 beta 参数的标准差分别是 tau_alpha 和 tau_beta ,残差标准差参数 tau_c 的估计为 6.1。简单起见,没有考虑截距项和斜率项的相关性,即不考虑小鼠出生时的重量和生长率的相关性,一般来说,应该是有关系的。函数 lme() 的输出结果中给出了截距项和斜率项的相关性为 -0.343,随机截距和随机斜率的相关性为 -0.159。
计算与 Stan 输出中的截距项 alpha_c 对应的量,结合函数 lme() 的输出,截距、斜率加和之后,如下
值得注意,Stan 代码中对时间 days 做了中心化处理,即 \(x_t - \bar{x}\),目的是降低采样时参数 \(\alpha_i\) 和 \(\beta_i\) 之间的相关性,而在拟合函数 lme() 中没有做处理,因此,结果无需转化,而且更容易解释。
#>
#> Call:
#> lm(formula = weight ~ days, data = rats_data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -38.253 -11.278 0.197 7.647 64.047
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 106.5676 3.2099 33.20 <2e-16 ***
#> days 6.1857 0.1331 46.49 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 16.13 on 148 degrees of freedom
#> Multiple R-squared: 0.9359, Adjusted R-squared: 0.9355
#> F-statistic: 2161 on 1 and 148 DF, p-value: < 2.2e-1634.2.4 lme4
当采用 lme4 包拟合数据的时候,发现输出结果与 nlme 包几乎相同。
#> Linear mixed model fit by REML ['lmerMod']
#> Formula: weight ~ days + (days | rats)
#> Data: rats_data
#>
#> REML criterion at convergence: 1095.4
#>
#> Scaled residuals:
#> Min 1Q Median 3Q Max
#> -2.6371 -0.5395 0.1188 0.4927 2.6091
#>
#> Random effects:
#> Groups Name Variance Std.Dev. Corr
#> rats (Intercept) 115.4239 10.7435
#> days 0.2607 0.5106 -0.16
#> Residual 36.1753 6.0146
#> Number of obs: 150, groups: rats, 30
#>
#> Fixed effects:
#> Estimate Std. Error t value
#> (Intercept) 106.5676 2.2978 46.38
#> days 6.1857 0.1056 58.58
#>
#> Correlation of Fixed Effects:
#> (Intr)
#> days -0.34334.2.5 blme
blme 包基于 lme4 包拟合贝叶斯线性混合效应模型。
rats_blme <- blme::blmer(
weight ~ days + (days | rats), data = rats_data,
resid.prior = point, cov.prior = NULL
)
summary(rats_blme)#> Resid prior: point(value = 1)
#> Prior dev : 0
#>
#> Linear mixed model fit by REML ['blmerMod']
#> Formula: weight ~ days + (days | rats)
#> Data: rats_data
#>
#> REML criterion at convergence: 3938.2
#>
#> Scaled residuals:
#> Min 1Q Median 3Q Max
#> -16.7740 -3.3490 0.9875 2.7505 14.0468
#>
#> Random effects:
#> Groups Name Variance Std.Dev. Corr
#> rats (Intercept) 157.2001 12.5379
#> days 0.3325 0.5766 -0.34
#> Residual 1.0000 1.0000
#> Number of obs: 150, groups: rats, 30
#>
#> Fixed effects:
#> Estimate Std. Error t value
#> (Intercept) 106.5676 2.2977 46.38
#> days 6.1857 0.1056 58.58
#>
#> Correlation of Fixed Effects:
#> (Intr)
#> days -0.34334.2.6 INLA
library(INLA)
rats_inla <- inla(weight ~ 1 + days + f(rats, days, model = "iid"),
data = rats_data, control.predictor = list(compute = TRUE))
summary(rats_inla)#>
#> Call:
#> c("inla.core(formula = formula, family = family, contrasts = contrasts,
#> ", " data = data, quantiles = quantiles, E = E, offset = offset, ", "
#> scale = scale, weights = weights, Ntrials = Ntrials, strata = strata,
#> ", " lp.scale = lp.scale, link.covariates = link.covariates, verbose =
#> verbose, ", " lincomb = lincomb, selection = selection, control.compute
#> = control.compute, ", " control.predictor = control.predictor,
#> control.family = control.family, ", " control.inla = control.inla,
#> control.fixed = control.fixed, ", " control.mode = control.mode,
#> control.expert = control.expert, ", " control.hazard = control.hazard,
#> control.lincomb = control.lincomb, ", " control.update =
#> control.update, control.lp.scale = control.lp.scale, ", "
#> control.pardiso = control.pardiso, only.hyperparam = only.hyperparam,
#> ", " inla.call = inla.call, inla.arg = inla.arg, num.threads =
#> num.threads, ", " keep = keep, working.directory = working.directory,
#> silent = silent, ", " inla.mode = inla.mode, safe = FALSE, debug =
#> debug, .parent.frame = .parent.frame)" )
#> Time used:
#> Pre = 0.581, Running = 0.308, Post = 0.026, Total = 0.915
#> Fixed effects:
#> mean sd 0.025quant 0.5quant 0.975quant mode kld
#> (Intercept) 106.568 1.546 103.532 106.568 109.604 106.568 0
#> days 6.186 0.125 5.940 6.186 6.431 6.186 0
#>
#> Random effects:
#> Name Model
#> rats IID model
#>
#> Model hyperparameters:
#> mean sd 0.025quant 0.5quant
#> Precision for the Gaussian observations 0.017 0.002 0.013 0.017
#> Precision for rats 3.274 1.551 1.210 2.962
#> 0.975quant mode
#> Precision for the Gaussian observations 0.023 0.017
#> Precision for rats 7.167 2.420
#>
#> Marginal log-Likelihood: -590.38
#> is computed
#> Posterior summaries for the linear predictor and the fitted values are computed
#> (Posterior marginals needs also 'control.compute=list(return.marginals.predictor=TRUE)')34.3 习题
-
四个组的重复测量数据,如下表所示,建立贝叶斯线性混合效应模型/分层正态模型分析数据,与 nlme 包拟合的结果对比。
表格 34.2: 实验数据 编号 第1组 第2组 第3组 第4组 1 62 63 68 56 2 60 67 66 62 3 63 71 71 60 4 59 64 67 61 5 65 68 63 6 66 68 64 7 63 8 59 \[ \begin{aligned} y_{ij} \sim \mathcal{N}(\theta_i, \sigma^2) &\quad \theta_i \sim \mathcal{N}(\mu, \tau^2) \\ (\mu,\log \sigma, \tau) &\sim \mathrm{uniform\ prior} \\ i = 1,2,3,4 &\quad j = 1,2, \ldots, n_i \end{aligned} \]
\(y_{ij}\) 表示第 \(i\) 组的第 \(j\) 个测量值,\(\theta_i\) 表示第 \(i\) 组的均值,\(\mu\) 表示整体的均值,\(\sigma^2\) 表示组内的方差,\(\tau^2\) 表示组内的方差。
#> Linear mixed-effects model fit by REML #> Data: dat #> AIC BIC logLik #> 121.7804 125.1869 -57.89019 #> #> Random effects: #> Formula: ~1 | group #> (Intercept) Residual #> StdDev: 3.419288 2.366309 #> #> Fixed effects: y ~ 1 #> Value Std.Error DF t-value p-value #> (Intercept) 64.01266 1.780313 20 35.95584 0 #> #> Standardized Within-Group Residuals: #> Min Q1 Med Q3 Max #> -2.18490896 -0.59921167 0.09332131 0.54077636 2.17507789 #> #> Number of Observations: 24 #> Number of Groups: 4随机效应(组间标准差)\(\tau^2\) 3.419288 、残差效应(组内标准差)\(\sigma^2\) 2.366309。截距 \(\mu\) 64.01266 代表整体的均值。各组的均值如下:
-
基于 lme4 包中学生对老师的评价数据
InstEval建立(广义)线性混合效应模型分析数据。将响应变量(学生评价)视为有序的离散型变量,比较观察两个模型拟合效果(lme4、GLMMadaptive、spaMM 都不支持有序的响应变量,brms 则支持各类有序回归,使用语法与 lme4 完全一样。但是,由于数据规模比较大,计算时间数以天计,可考虑用 Stan 直接编码)。再者,从 Stan 实现的贝叶斯模型来看,感受 Stan 建模的灵活性和扩展性。(nlme 包不支持此等交叉随机效应的表达。)#> 'data.frame': 73421 obs. of 7 variables: #> $ s : Factor w/ 2972 levels "1","2","3","4",..: 1 1 1 1 2 2 3 3 3 3 ... #> $ d : Factor w/ 1128 levels "1","6","7","8",..: 525 560 832 1068 62 406 3 6 19 75 ... #> $ studage: Ord.factor w/ 4 levels "2"<"4"<"6"<"8": 1 1 1 1 1 1 1 1 1 1 ... #> $ lectage: Ord.factor w/ 6 levels "1"<"2"<"3"<"4"<..: 2 1 2 2 1 1 1 1 1 1 ... #> $ service: Factor w/ 2 levels "0","1": 1 2 1 2 1 1 2 1 1 1 ... #> $ dept : Factor w/ 14 levels "15","5","10",..: 14 5 14 12 2 2 13 3 3 3 ... #> $ y : int 5 2 5 3 2 4 4 5 5 4 ...- 因子型变量
s表示 1-2972 位参与评分的学生。 - 因子型变量
d表示 1-2160 位上课的讲师。 - 因子型变量
dept表示课程相关的 1-15 院系。 - 因子型变量
service表示讲师除了授课外,是否承担其它服务。 - 数值型变量
y表示学生给课程的评分,1-5 分对应从坏到很好。
# 数值型的响应变量 fit_lme4 <- lme4::lmer(y ~ 1 + service + (1 | s) + (1 | d) + (1 | dept), data = InstEval) summary(fit_lme4)#> Linear mixed model fit by REML ['lmerMod'] #> Formula: y ~ 1 + service + (1 | s) + (1 | d) + (1 | dept) #> Data: InstEval #> #> REML criterion at convergence: 237733.8 #> #> Scaled residuals: #> Min 1Q Median 3Q Max #> -3.0597 -0.7478 0.0404 0.7723 3.1988 #> #> Random effects: #> Groups Name Variance Std.Dev. #> s (Intercept) 0.105998 0.32557 #> d (Intercept) 0.265221 0.51500 #> dept (Intercept) 0.006912 0.08314 #> Residual 1.386500 1.17750 #> Number of obs: 73421, groups: s, 2972; d, 1128; dept, 14 #> #> Fixed effects: #> Estimate Std. Error t value #> (Intercept) 3.28259 0.02935 111.858 #> service1 -0.09264 0.01339 -6.919 #> #> Correlation of Fixed Effects: #> (Intr) #> service1 -0.152 - 因子型变量